Tldr

文章链接

这篇文章的前置版本可以查看 IPASIR 介绍，本文拓展了 IPASIR，加入了外部传播或者用户传播（UP）的拓展

Overview

我们所提出的扩展允许用户：

在搜索过程中检查 trail 的变更并接收相关通知
在求解过程中无需重启搜索即可向问题中添加子句
基于外部知识直接传播文字，而无需显式添加原因子句（即采用延迟的按需解释机制）。

在本文中，我们将外部传播统一称之为 UP，注意区分单元传播（Unit Propagate）

UP 的理解

我们可以将 UP 理解为外部传播器，以 SMT 的框架为例子，SMT 的内部核心为 SAT 求解器，本质上我们是做了增量式求解，通过 SMT 的理论求解器为 SAT 求解引入更多的 lemma，从而解决问题，这里我们可以将 SMT 看作是外部传播

Extend State

回顾 IPASIR 状态转移，在 UP 中，我们将 SOLVING 状态拓展为五个独立的状态，如下图所示，在每个状态转换时，都会触发相应的回调函数（cb_ 前缀的函数）：

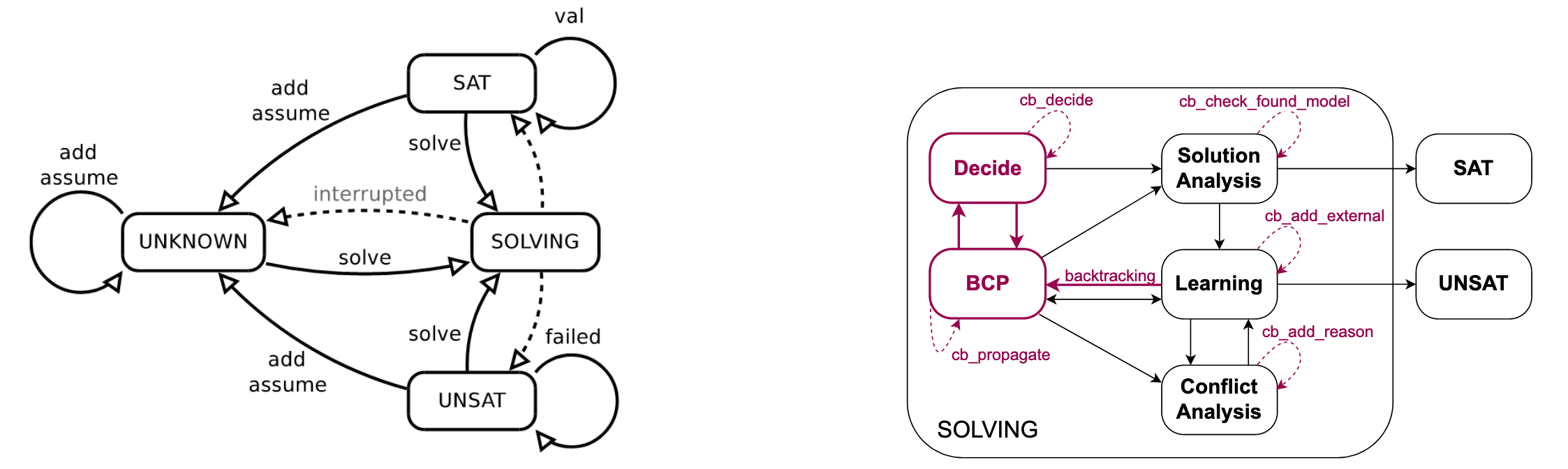
CDCL 由 BCP 与 Decide 迭代进行，直到出现以下两种情况之一：要么某个子句在当前赋值下被证伪，要么所有变量都被赋予真值：

求解器会转入冲突分析状态。在此状态下，我们会进行归结与子句学习，如果学习到的子句为空，则求解器转入 UNSAT 状态；否则，它将回溯到更低的决策级别，并重新开始 BCP。
否则，一旦找到一个完整的赋值（即所有变量均被赋值且没有冲突），标准的 CDCL 求解器将转入 SAT 状态。然而，在存在 UP 的情况下，我们引入了一个称为解分析的人工状态，作为转入 SAT 状态之前的一个中间状态。

Configuration and Management

我们在求解器未进入到 SOLVING 阶段时，可以通过接口 connect_external_propagator 来连接一个自定义的 UP ，UP 也可以通过接口 disconnect_external_propagator 来断开与求解器的连接（注意，一个求解器只能连接一个 UP）
当一个 UP 被连接到求解器时，我们可以通过接口 add_observed_var 来让求解器观测一个变量，即使此时求解器处于 SOLVING 阶段；而不在求解阶段时，我们可以通过接口 remove_observed_var 来删除一个已观测的变量

观测变量

观测变量会被冻结（不会被简化操作删除），且其赋值的变化会通知 UP，且所有的 IPASIR - UP 调用都只涉及观测变量。

phase 函数允许在对指定变量进行决策时强制给定该变量的特定相位，实现例如：

1
void Internal::phase (int lit) {
2
  const int idx = vidx (lit);
3
  signed char old_forced_phase = phases.forced[idx];
4
  signed char new_forced_phase = sign (lit);
5
  if (old_forced_phase == new_forced_phase) {
6
    LOG ("forced phase remains at %d", old_forced_phase * idx);
7
    return;
8
  }
9
  if (old_forced_phase)
10
    LOG ("overwriting old forced phase %d", old_forced_phase * idx);
11
  LOG ("new forced phase %d", new_forced_phase * idx);
12
  phases.forced[idx] = new_forced_phase;
13
}

当然我们也可以通过 unphase 来解除这个约束

is_decision 用于查询被观测的变量是否为决策赋值
force_backtrack 当一个新的决策被做出之前，我们可以通过调用这个函数来让求解器强制回溯到一个特定的决策层

回溯时如何维护 UP 中拿到的 trail

回溯到发生变更的最低决策层，并从此层级开始重新通知每个决策层。这样 SAT 求解器可维持其运行逻辑，而 UP 能重构自身的栈式 trail。

另一种方案是在 SAT 求解器内部将 trail 作为栈处理。例如，只要回溯层高于实际赋值层，乱序赋值可在每次回溯后重新分配。增量惰性回溯（ILB）和 trail-reuse 等技术旨在通过识别可复用先前搜索的trail 片段来避免重复计算。若复用了先前 trail的前缀，只需回溯至最后保留的决策层即可向 UP 传递信息。

Tip

通常用户无需了解 SAT 求解器使用的增量技术即可正确使用。但有一些特殊情况：

例如用户可能在两次求解调用间清理传播器，而求解器因 ILB 技术未必重启搜索。

Collaborate with CDCL

如果我们将 SAT 求解器的状态看作是一个二元组 $F ∣∣ M$ ，其中 $F$ 为原问题公式， $M$ 为当前的部分赋值，显然对于 SAT 而言， $F$ 的改变至关重要，这是 SAT 在意的基础，而对于外部传播器而言（例如 $C D C L (T)$ ）显然 $M$ 更为重要，这影响这外部理论的传播，因此我们需要在外部捕获求解时 trail 的实时变化。

由于 CaDiCaL 对有内部文字与外部文字的区分（用于内存的优化），我们无法直接给出完整的 trail 路径（否则性能开销过大），于是我们通过迂回的方式，用 notify 来给予外部传播器赋值信息：

当一个被观测变量被赋值时，求解器通过 notify_assignment 来提示 UP，注意，这个赋值带有持久性，意味着在回溯时，我们必须确保其赋值不会被改变
当我们决策一个新变量（进入新的决策层）时，求解器通过 notify_new_decision_level 来提示 UP，但注意，其不提示具体到了哪一个决策层，而只是提示决策发生了
同理，在发生回溯时，我们也会通过 notify_backtrack 来提示 UP，但这里我们会提供其回跳到了哪一层

而 UP 通过回调函数来影响 CDCL，主要体现在：

每次决策前，我们会调用 cb_decide 函数，对选定的变量和相位执行我们特定的选择；需要注意的是，只有在所有假设都满足之后，我们才能开始调用这个函数。（==注意，我们也可以通过 force_backtrack 来强制求解器回溯状态，从而调用 cb_decide==）

Attention

此外，phase 和 unphase 函数允许用户与求解器共享关于变量的额外知识。

目前没有标准化方法供用户访问求解器中变量的分数或顺序（也就是 VSIDS 的堆以及 VMTF 队列），标准化低开销访问此类信息仍是一个 Open Problem

在 BCP 时，我们调用 cb_propagation 函数来提供额外的待传播文字。需要注意的是，这个函数只返回一个待传播的文字，且此时不需要传播子句

在冲突分析过程中，如果我们通过 cb_propagation 提供了一个待传播文字（propagated_lit），且这个文字和冲突相关，求解器会通过 cb_add_reason_clause_lit 函数向用户请求相应的原因子句，每次请求一个文字（注意，我们要求 propagated_lit 必须在这个子句中）， ==我们通过成员变量 are_reasons_forgettable 来控制是否能删除这些原因子句==
当求解器确定了一个完整的赋值且没有违反任何现有子句时（即找到了一个 SAT 解），就会调用 cb_check_found_model 函数。这个函数的作用是让 UP 验证 SAT 模型是否与用户的外部约束一致。如果不一致，可以在不重启搜索的情况下向问题中添加额外的子句。==注意，这个函数被成员变量 is_lazy 控制，默认为 false，如果为 true 那么才会在找到 SAT 解时调用这个函数==
当求解器完成 BCP 之后（在决策之前），或者当函数 cb_check_found_model 返回 false 时，用户可以向问题中添加新的子句。函数 cb_has_external_clause 用于指示是否有新的子句要添加，参数允许用户指定外部子句的“可遗忘性”。可遗忘子句允许在子句数据库缩减期间被 SAT 求解器删除，但求解器决定实际删除时机（例如，单位子句即使可遗忘也不会被删除）。如果子句不可遗忘（参数为 false），求解器认为该子句不可约简。（子句被直接加入到问题中，然而如果设置为可遗忘，可以认为被加入到了子句库中）
通过 cb_add_external_clause_lit 逐文字地添加该子句

Attention

目前，用户无法强制删除子句或收到外部子句删除的通知。

Finding Fixed Assignments

根据具体应用场景，用户若能知晓 SAT 求解器做出的某个赋值将永久保持不变（即该赋值已固定），通常能带来益处。这使得用户可基于这些固定赋值执行进一步优化，从而简化自身约束条件与问题表达。

当前 IPASIR-UP 的通知功能仅反馈（取消）赋值状态。

我们只需要接入 FixedAssignmentListener，当任何变量被固定时会主动发送通知。

1
class FixedAssignmentListener {
2
public:
3
  virtual ~FixedAssignmentListener () {}
4

5
  virtual void notify_fixed_assignment (int) = 0;
6
};

求解器在 mark_fixed 中调用这个函数，通知外部传播器（注意，SAT 求解器只会在学习到单元子句/传播单元子句时调用 mark_fixed）

Export Learned Clause

IPASIR-UP 支持通过 Learner 来导出学习子句，其接口如下：

1
class Learner {
2
public:
3
  virtual ~Learner () {}
4
  virtual bool learning (int size) = 0;
5
  virtual void learn (int lit) = 0;
6
};

我们通过 learning 函数来判断是否可以导出学习子句，其中 size为准备好的学习子句的长度，若返回 true，则我们会通过 learn 函数来逐文字的导出学习子句；否则不导出。

注意，SAT 求解器会在生成学习子句时，通过以下调用来判断是否需要导出，例如：

1
void Internal::analyze () {
2
// ....
3
    if (external->learner)
4
      external->export_learned_large_clause (clause);
5
// ....
6
}

1
void External::export_learned_large_clause (const vector<int> &clause) {
2
  assert (learner);
3
  size_t size = clause.size ();
4
  assert (size <= (unsigned) INT_MAX);
5
  if (learner->learning ((int) size)) {
6
    LOG ("exporting learned clause of size %zu", size);
7
    for (auto ilit : clause) {
8
      const int elit = internal->externalize (ilit);
9
      assert (elit);
10
      learner->learn (elit);
11
    }
12
    learner->learn (0);
13
  } else
14
    LOG ("not exporting learned clause of size %zu", size);
15
}

Tip

一般来说我们只需要在 learning 中写上自己的判断条件即可

Known Issue

IPASIR-UP 支持更细粒度的增量 SAT 求解方式，新子句不仅可以在两次求解调用之间添加，还可以在求解过程中添加。然而添加新子句存在以下两个问题：

每次 UP 提供子句时遍历整个重构栈可能成本过高（因为 SAT 求解器自身存在预处理技术）
SAT 求解器的技术需要在找到简化公式的满足解后执行额外的解重构步骤（例如为消除的变量赋值/翻转一些拓展变量的值）。被翻转的变量可能位于 trail 中的任何决策层。由于 UP 对 trail 具有类似栈的视图，用户无法在不回溯到相应级别的情况下取消分配和重新分配这些变量。

目前，IPASIR-UP 假设 observed 的变量在 SAT 中被冻结，并且每当通过 add_observed_var 添加变量时，它对于重构栈是无影响的。这确保了在添加外部子句时不需要额外的恢复步骤，并且在找到的解中不会翻转变量赋值。

如果用户将一个子句定义为可遗忘，并且求解器决定删除它，它将在证明中显示为冗余子句的正常删除步骤，在这些情况下，需要在产生的证明中区分外部可遗忘子句和真正冗余的子句。

Conclusion

本质上就是暴露了一个更加 User-Friendly 的接口，让那些将 SAT Solver 作为 core 的其他求解器更加容易编写

Appendix

文章也举了一个例子 SAT modulo Symmetries(SMS)

SMS 是近期提出的一种基于 SAT 的框架，用于穷举生成具有特定属性的组合对象（如图或超图），同时排除相同对象的同构副本（无同构生成）。与首先生成候选对象再检测的”生成-测试”方法相比，SMS 能直接生成满足要求的无同构对象。

生成图对象

通过为每个顶点对 $(u, v)$ 定义边存在性变量 $e_{u, v}$ 来表达图属性。为避免生成同构副本，SMS 引导求解器生成规范对象，例如要求邻接矩阵满足字典序最小化。¹

如何使用

可以参考示例

本质上就是用一个类去实现 IPASR-UP 的接口即可

最小化方法，可以将邻接矩阵按照行展开，列成一个二进制字符序列，比较这个序列的字典序即可 ↩

また夏を追う

最近的笔记

GTest 单元测试模板

如何知道实验什么时候结束

探索

IPASIR-UP: User Propagators for CDCL

Overview

Extend State

Configuration and Management

Collaborate with CDCL

Finding Fixed Assignments

Export Learned Clause

Known Issue

Conclusion

Appendix

🕸️ 关系图谱

目录

また夏を追う

最近的笔记

GTest 单元测试模板

如何知道实验什么时候结束

探索

IPASIR-UP: User Propagators for CDCL

Overview

Extend State

Configuration and Management

Collaborate with CDCL

Finding Fixed Assignments

Export Learned Clause

Known Issue

Conclusion

Appendix

Remarque

🕸️ 关系图谱

目录