SAT 问题简介

复习一些数学知识

Note

在最开始，我们复习一些基础的离散数学，主要是一元逻辑部分，我们默认读者有基本的位运算基础，如果没有的话，可以查看下面进行学习

位运算 \&, |, \neg，其中，前面两种为二元运算，非运算为一元运算，其真值表的变化为：

y&x	0	1
0	0	0
1	0	1

y|x	0	1
0	0	1
1	1	1

$\neg$x	0	1
	1	0

我们首先引入一个记号 $\mathbb{B}=\{0,1\}$，这是一元逻辑中所有变量的定义域

我们称 $\forall x\in \mathbb{B}$ 的 $x$ 为布尔变量，其取值只有 0/1，也就是真/假，对于单个布尔变量，我们有一元运算如下：

$\forall x\in \mathbb{B},\neg x\in \mathbb{B}$ 其中，$\neg$ 为非运算。

接着，我们定义布尔变量之间的运算，其只有 $+,\cdot$ 两类运算，我们在下面引入记号并详细：

1. $\forall x,y\in \mathbb{B},x\ne y$，我们有 $x+y=y+x=x\vee y\in \mathbb{B}$，其中 $\vee$ 表示或运算
2. $\forall x,y\in \mathbb{B},x\ne y$，我们有 $xy=yx=x\wedge y\in \mathbb{B}$ ，其中 $\wedge$ 表示与运算

由此，我们可以定义如下布尔函数：

$$F(x_1,x_2,\dots ,x_n):{\mathbb{B}}^n\to \mathbb{B}$$

$x_1,x_2,\dots ,x_n$ 通过上文中定义的三种运算结合构成此布尔函数，例如：

$$F(x_1,x_2,x_3)=(x_1\vee x_2)\wedge x_3\vee \neg (x_2\vee x_1\wedge \neg x_3)$$

可满足问题（SAT 问题）

首先，我们引入一些 SAT 问题中的记号

CNF

我们通过一些运算规则与定理，可以将任意的布尔函数都转化为合取范式的形式（ CNF），例如上式可以转为：

$$F^{\prime }(x_1,x_2,x_3)=(x_1\vee \neg x_2\vee x_3)\wedge (\neg x_1\vee x_3)\wedge (\neg x_2\vee x_3)$$

也就是通过 $\wedge$ 连接的若干个 $\vee$ 式，这里：

• 我们将 $\vee$ 式称为 子句（clause），每个子句都是由若干个 $l_i\in \{x_i,\neg x_i\}$ 组成
• 我们将 $l_i$ 称为变量 $x_i\in \mathbb{B}$ 对应的 文字（literal），若 $l_i=x_i$，我们将其称为正文字，若 $l_i=\neg x_i$ ，我们将其称为反文字

更进一步的，在 SAT 问题中，我们还有以下名词：

• 极性（Polarity），通常指变量在子句中的出现形式，换而言之，正文字就是极性为正，反文字就是极性为负
• 赋值 （Assignments），我们可以使用此函数来表示 $\Phi :X\to {\mathbb{B}}^n$，其中 $X=\{x_1,x_2,\dots ,x_n\}$，所有变量 $x_i$ 赋值后得到的一组有序向量，我们将其称为 CNF 的一组赋值

SAT 定义

这样，我们可以轻松的导出 SAT 问题的定义：

SAT 问题

给定一个 CNF ：$\mathcal{F}(x_1,x_2,\dots ,x_n)$，问是否存在一组赋值 $\varphi$ 使得 $\mathcal{F}=1$ 成立

值得一提的是，目前还找不到一种多项式时间的算法来解决这个问题，事实上，著名的未解问题 “P 是否等于 NP” 等价于询问这样的算法是否存在。

SAT 问题可以被认为是 “所有 NP 完全（NP-Complete）问题的起源”

我们在这里不探讨过多的计算复杂性相关的内容，如果你对这些内容感兴趣，可以阅读以下内容入门

• introduction to the theory of computation
• 怎么理解 P 问题和 NP 问题？
• 从 OIer 的角度解释什么是 P 问题、NP 问题和 NPC 问题

小知识

判定一个 CNF 是 UNSAT（不可满足的）会比判断其 SAT （可满足）在工程上要困难，也就是耗时会更多

这是因为判断 UNSAT 本质上是一个证明，我们必须证明在整个解空间内不存在一组赋值 $\varphi$ 使得 $\mathcal{F}=1$

实例

我们常用 .cnf 文件来描述一个 SAT 问题，例如：

1
p cnf 3 2
2
1 2 0
3
-1 3 0
4
2 -3 0

这个 .cnf 文件表示当前问题有 $3$ 个变量，$2$ 条子句组成，公式的构成为：

$$(x_1\vee x_2)\wedge (\neg x_1\vee x_3)\wedge (x_2\vee \neg x_3)$$

我们在后面的举例中会经常使用下面这个例子：

1
p cnf 7 8
2
-5 7 0
3
-1 -5 6 0
4
-1 -6 -7 0
5
-1 -2 5 0
6
-1 -3 5 0
7
-1 -4 5 0
8
-2 -3 -4 5 0
9
-1 2 3 4 5 -6 0

用图表示如下：

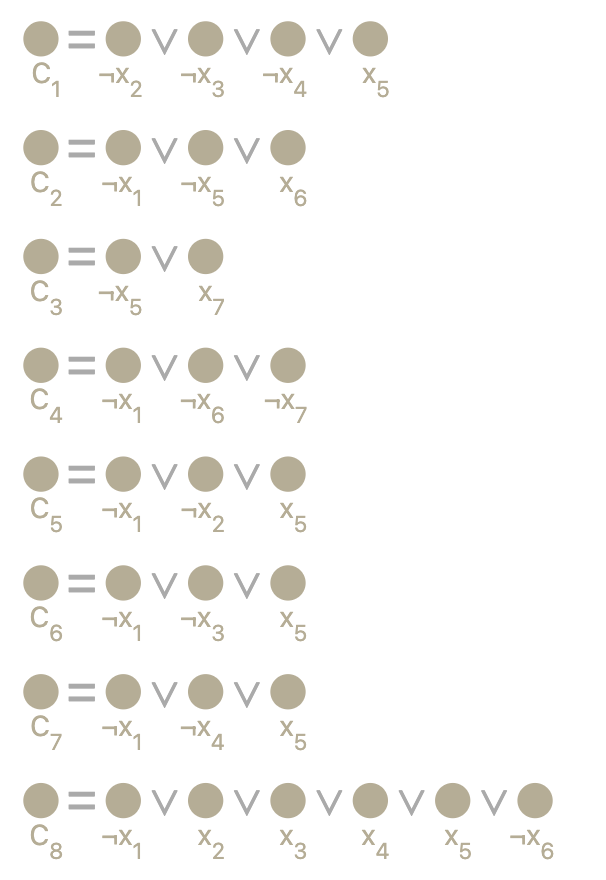
我们通过 $lit@level$ 的形式来说明赋值情况

Example

例如 $(x_1@1,\neg x_2@2)$ 表示我们第一次赋值将 $x_1$ 赋为真，第二次将 $x_2$ 赋值为假