Motivate

在 SAT 的精确算法中，最重要的步骤之一是布尔约束传播（Boolean Constraint Propagation, BCP），其在求解过程中甚至占用了 $90%$ 的时间¹。

BCP 简介

当一个变量 $v$ 被赋值后 $v \leftarrow ⊥$ ，BCP 会检查所有包含变量 $v$ 的子句，并更新这些子句的状态。当子句未满足且只剩下一个文字未被赋值，那么 BCP 将这个文字赋值为 $⊤$ （也就是为变量赋值）

然而，最初版本的 BCP 会在每次赋值后，扫描所有包含该变量假文字的子句，这非常低效，因为子句库中含有大量子句，我们并不需要每次都去扫描一遍（即使我们维护了一个高效的链表来找到这些相关的子句）

Optimization

理论基础

对于一个子句，我们只需关注它内部的某一个文字。只要这个文字为真，整个子句就满足了，无需理会该子句或其他子句中其他文字的情况。 ²

在这里我们提出了观察字 （watched literal ）的概念，其工作原理如下：

我们假定，对每个子句 $c$ ，其观察字表示为 $w [c]$ ，初始为子句的第一个文字，对于每个文字 $l$ ，我们都有一个链表来描述其观察的子句，将其表示为 $W [l]$ 。

当变量 $v \leftarrow ⊤$ ，我们找到那些观察字为 $\overset{v}{ˉ}$ 的子句 $c$ ，对于每个子句：

我们向后寻找一个未赋值为假（未被赋值/赋值为真）的文字 $u$ ，将 $w [c] \leftarrow u$ ，这样子句有了一个新的有效观察字 $w [c]$ （注意需要维护 $W [u], W [v]$ ）
如果只有一个这样的文字，那么我们可以通过传播进行赋值： $u \leftarrow ⊤$ ，
如果我们没有找到这样的文字 $u$ ，说明子句 $c$ 没有一个文字为真，此时冲突发生，直接返回

这里我们用一个简单的图例来描述过程：

F = (\overset{ˉ}{1} \lor \overset{ˉ}{2}) \land (\overset{ˉ}{1} \lor 2 \lor \overset{ˉ}{3}) \land (3 \lor \overset{ˉ}{4} \lor \overset{ˉ}{5})

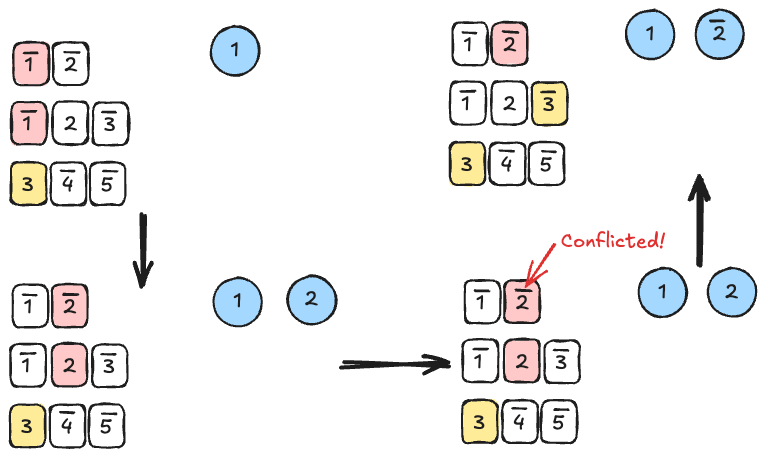
图中染色部分为观察字，右侧只显示赋值为真的文字

更进一步的，在工程上我们提出了双观察字，因为在寻找新的观察字时，我们可能仍然需要扫描整个子句，最坏情况下时间复杂度是 $O (∣ C ∣)$ 。

为每个子句同时维护两个被观察的文字，只要这两个观察字中有一个为真，子句就是满足的，

本质上我们只是用了双指针的方法来优化传播的性能：

假定子句 $c$ 的观察字被初始化为最开始的两个文字 $l_{1}, l_{2}$ ，当其中一个观察字被赋值为假后 $l_{1} \leftarrow ⊥$

我们在后续的文字中找到一个未被赋值为假的文字，作为 $l_{1}$ 观察字的替换
如果不存在这样的文字，那么说明此时我们可以传播 $l_{2} \leftarrow ⊤$ ，而如果 $l_{2}$ 已经被赋值为假，此时我们发生了冲突，直接返回

Moskewicz, Matthew W. et al. “Chaff: engineering an efficient SAT solver.” Proceedings of the 38th Design Automation Conference (IEEE Cat. No.01CH37232) (2001): 530-535. ↩
Purdom, Paul Walton and Cynthia A. Brown. “An Analysis of Backtracking with Search Rearrangement.” SIAM J. Comput. 12 (1983): 717-733. ↩