基数约束 SAT 并行策略

Problem Partitioning via Proof Prefixes

Tip

前置知识：

1. Cube & Conquer
2. Clause Proof

这里简要解释：

1. Cube & Conquer 是一种并行方法，本质上是对解空间的一次静态划分，选择一个良好的变量序列作为假设（cube），将解空间划分为多个不相交的子集，然后每个解空间都通过一个线程独立求解
2. 子句证明（以 LRAT 为例）：本质上是 CNF 的证明序列，用于说明 UNSAT 为什么 UNSAT，通过不断对这个序列的子句做归结，能够导出空子句 $\perp$ 从而证明 UNSAT

主要贡献

我们假定证明是一组冗余子句序列（冗余意为加入/不加入改子句，对原公式的可满足性没有影响，学习子句均为冗余子句），那么证明前缀（Proof Prefixes）是指从证明起始处开始的一系列子句添加步骤序列。

既然我们要使用 Cube & Conquer，那么我们必须得选择出一个良好的划分序列来分解子问题，这里选择的标准为：变量出现次数，即某个变量在子句的添加步骤中被引用的频率。（即在证明前缀的子句中出现的次数）

这个选择标准基于两个发现：

1. 在非平凡（包含足够多步骤）的证明前缀中频繁出现的变量，往往会在证明后续部分持续高频出现（实验发现的）；
2. 对于已知存在有效划分的问题而言，划分变量通常在原始（未划分）公式生成的证明中具有较高出现频率。

静态划分

因此我们的做法十分简单：

首先，给定一组划分集合 $S=\{x_1,x_2,x_3,\dots ,x_d\}$ ，我们下一步是确定第 $d+1$ 个划分的变量是谁。

然而这样我们会生成 $2^d$ 个子问题（同样也有 $2^d$ 个证明前缀），这样的做法效率太低，于是，我们采取的策略为：

对于这 $2^d$ 个子问题，我们随机 sample $s$ 个子问题出来，对这 $s$ 个子问题进行证明前缀的生成，然后统计并得出第 $d+1$ 个变量，如下图所示：

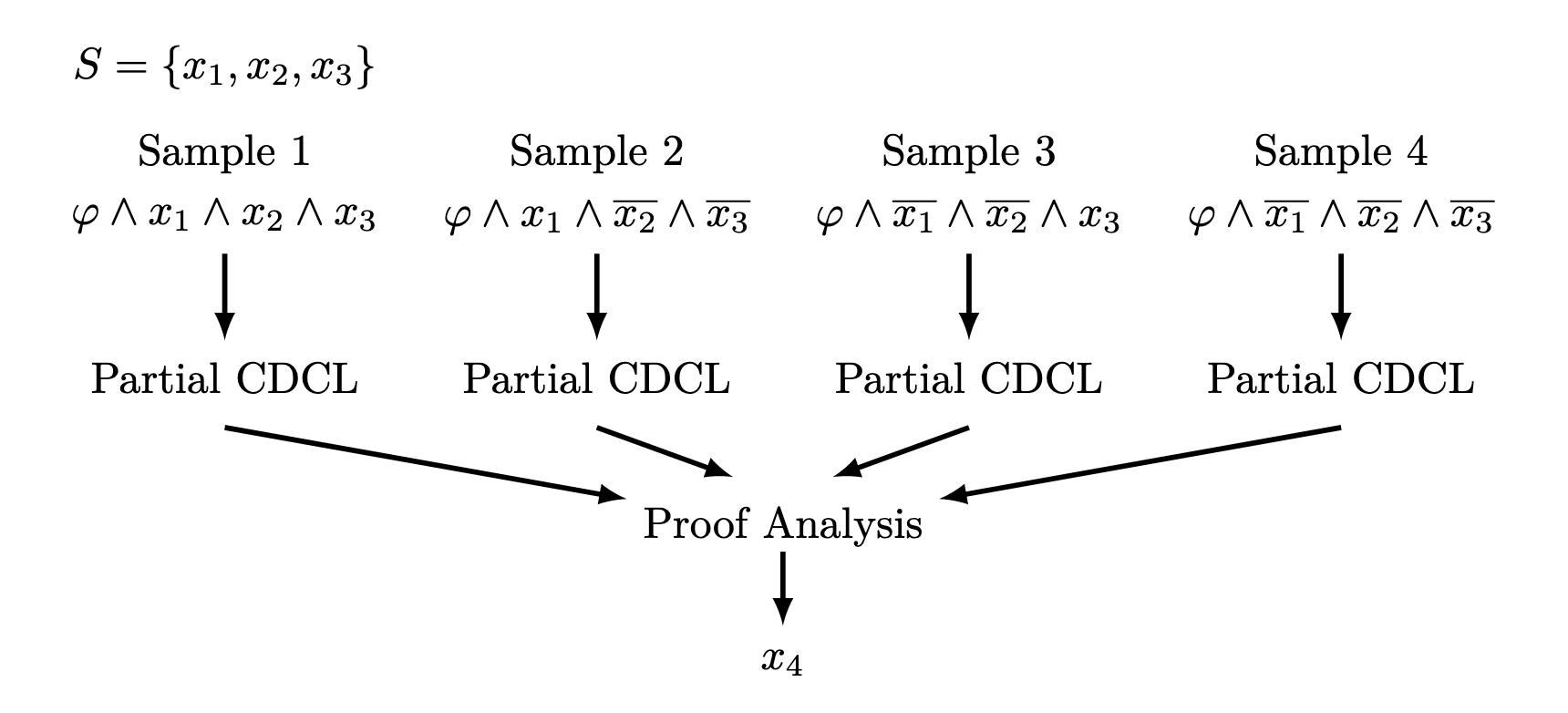
Attention

$x_4$ 的生成是需要统计所有 sample 子问题的证明前缀选择的，因此本质上带有短板效应

论文中的前缀生成阶段条件设置为：生成 100000 个前缀就可以截止了，在论文的 benchmark 表现都较好

基数约束并行

考虑 Totalizer 的编码方式，我们可以考虑以下二叉树来说明这个方法：

例如基数约束 $l_1+\cdots +l_{16}\le 7$，编码如下，附加单元子句 $\neg o_8$，其中辅助变量遵循 $c_{cnt}^{dep,id}$ 的命名方式

• 如果 $c_4^{1,1}$ 为真，那么表示 $l_1+\cdots +l_8\ge 4$ ，等价于 $l_9+\cdots +l_{16}\le 3$
• 如果 $c_4^{1,1}$ 为假，那么 $l_1+\cdots +l_8\le 3$ ，然而我们无法确定 $l_9\dots ,l_{16}$ 中的信息

如果我们对这些辅助变量进行赋值，那么可以立刻限制原始变量中的赋值情况（相当于对基数约束做分解）

而为了避免产生极其不平衡的子问题（即一边是由于边界冲突导致的极易求解，另一边则很难），算法试图让划分变量的取值“顺应”全局约束的比例

Example

取 $c_7^{1,1}$ 为真，那么就会导致 $l_9,\dots ,l_{16}$ 全部为假，从而得到一个非常容易的子问题，基本上不属于良好的划分

于是，针对度为 $k$ ，包含 $s$ 个变量的基数约束，在二叉树的第 $L$ 层，假定改层的每个节点均包含 $n$ 个计数器，我们通过全局比率：

$$Rk=\frac{k}{s}$$

附加公式

$$id=\lfloor Rk\times n\rfloor$$

来计算到底选这一层的哪个计数器

我们的做法形式化描述为以下步骤：

1. 首先计算全局比率 $Rk$
2. 对于 Totalizer，其每个内部节点都有 $n$ 个计数器变量（用来表示该节点子树中有多少个输入为真）。对于特定深度 $d$ 的某个节点，且该节点拥有 $n$ 个计数器，算法通过以下步骤选择划分变量： 3. 计算基准索引 $id$ 4. 奇数 ID 节点选择索引为 $id+1$ 的计数器，否则选择 $id$ 的计数器

Example

考虑上图中，$Rk=\frac{7}{16}$，假定我们现在想要 $6$ 个划分变量，那么我们从第一层开始往下找：

1. 在第 1 层的第 1 个节点，其含有 8 个计数器，那么我们拿到的划分变量为 $c_{\lfloor \frac{7}{16}\times 8\rfloor +1}^{1,1}$，即为 $c_4^{1,1}$
2. 第 1 层的第 2 个节点，其含有 8 个计数器，那么拿到的为 $c_3^{1,1}$

不断向深层横向变量，直到我们拿到的划分变量达到上限为止

这种“奇数加一，偶数不加”的策略是为了让同一深度上所有被选中的变量所代表的“计数总和”接近全局约束 $k$

Danger

目前这种并行划分方式只能用于 MaxSAT 类似的划分（因为只有一条基数约束）

总结

本质上感觉做的比较简单，但是确实解决了之前 基数约束SAT的精确求解器 中提到的求解 MaxSAT 类型例子速度慢（指常规的 CCDCL，而不是重编码的）